10.6.2 Statistical
Methods
10.6.2.1 Computation Magnitudes
If a random sample is taken in order to
inspect a large number of parts, a finite number of measured
values are obtained. If a sufficiently large number of measurements
is taken, a continuous curve can be drawn representing the
entirety of all parts, even those that were not measured.
The curves associated with distributions are distinguished
by their position, width and shape; they can occur next to
each other and can be superimposed. Data very often display
a normal distribution, also called a Gaussian
distribution or bell curve, due
to its form.
The normal distribution is mathematically described by the
two following variables.
Arithmetic mean:
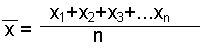
where n = number of values with individual values Xi from
X1 to Xn
Standard deviation:
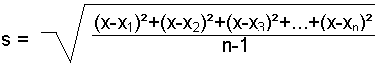
The mean value, x, is the centre of the normal distribution
curve and indicates the position of the distribution.
The standard deviation, s, describes the scattering of the
process. It is a measure of the width of the normal distribution
curve, and is the distance between the mean value, x, and
the inflection point of the normal distribution.
The area under the normal distribution curves is proportional
to the frequency with which the values occur. In the region
within ± 1 s around the mean value x, i.e. 2 s, the
hatched area underneath the normal distribution curve contains
68.26 % of all the values. The region ± 3 s around
the average value, that is 6s wide, covers 99.73 % of all
values. The points 3s from the mean value are defined as the
natural process boundaries.
|
|

