5.3.3.4 Weibull
modulus
Using a theory developed by Weibull, based
on the concept of the failure of the weakest link, the strength
distribution of ceramic materials can be described effectively
in mathematical terms. An important assumption is that the
failure is caused by a single "failure type" (structural
inhomogeneity). Weibull chose to describe the strength behaviour
using a special form of extreme value distribution; this was
later named the Weibull distribution in his honour.
This results in a definite relationship between mechanical
load and the failure probability of a part if the distribution
parameters are known. Using a level of strength at which the
failure probability becomes 63.2 % (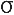 0),
the Weibull modulus (m) becomes a measure of the distribution
of strengths. The higher the Weibull modulus is, the more
consistent the material (which means that uniform "defects"
are evenly distributed throughout the entire volume) and also
the narrower the probability curve of the strength distribution.
Today, values between 10 < m < 20 are typically achieved.
These values are determined for ceramic materials usually
using the four-point bending method, since measuring the tensile
strength of these materials is extremely difficult. 0),
the Weibull modulus (m) becomes a measure of the distribution
of strengths. The higher the Weibull modulus is, the more
consistent the material (which means that uniform "defects"
are evenly distributed throughout the entire volume) and also
the narrower the probability curve of the strength distribution.
Today, values between 10 < m < 20 are typically achieved.
These values are determined for ceramic materials usually
using the four-point bending method, since measuring the tensile
strength of these materials is extremely difficult.
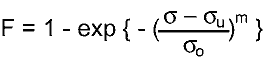
| F = failure
probability |
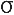 = stress
= stress |
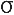 u
= minimum strength u
= minimum strength |
m = Weibull modulus |
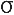 0
= Location parameter of the Weibull distribution, strength
at 63.2% failure probability; in the Weibull distribution
this plays the role of the mean value in a normal distribution. 0
= Location parameter of the Weibull distribution, strength
at 63.2% failure probability; in the Weibull distribution
this plays the role of the mean value in a normal distribution.
Typically, 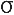 u
= 0 is used u
= 0 is used |
Since the number of possible defects in
this ceramic is dependent on the volume of the part, the volume
under load must be taken into account. The strength of larger
parts is thus less than what is measured on test samples.
However, with large volumes under load, a larger Weibull modulus
results in higher load capacity. Using Weibull statistics,
the following component strength results from the volume relationship:
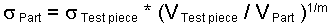
The volume under stress is to be inserted
here for the component volume, and the stress distribution
must be identical (e.g. 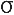 tensile
or tensile
or 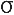 4pb).
This relationship does not apply to compressive stress! 4pb).
This relationship does not apply to compressive stress!
Test procedures for determining the Weibull modulus are specified
in DIN EN 843-5 and DIN 51 110-3.
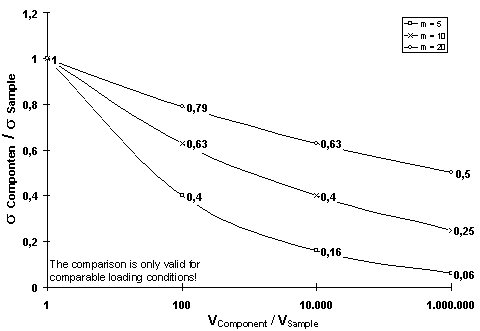
Figure 85: Relationship between component
size and strength for
different values of Weibull modulus, m
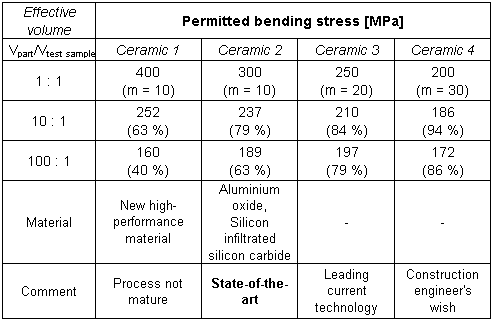
Table 10: Comparison of the strengths of components
and test pieces for
different strength scatters (Weibull modulus, m)
|
|

